목차
탐색이란
여러 자료 중에서 원하는 자료를 찾는 작업입니다. 탐색의 단위는 항목으로 key로 항목을 구분합니다. 이를 탐색 키(search key)라고 합니다. 탐색이란 탐색 키와 데이터로 이루어진 항목 중에서 원하는 탐색 키를 가지고 있는 항목을 찾는 것입니다.
순차 탐색
순차 탐색 (swquential search)
정렬되지 않은 배열의 항목들을 처음부터 마지막까지 하나씩 검사하여 원하는 항목을 찾아가는 방법입니다.
int seq_search(int key, int low, int high) {
int i;
for (i=low; i<=high; i++) {
if (list[i]==key)
return i; // 탐색 성공 시
return -1; // 탐색 실패 시
}
}
모든 키가 탐색될 확률이 동일하다고 가정하면 평균 비교 횟수는 (1+2+ … + n)/n = (n+1)/2 입니다. 따라서 탐색이 성공할 경우 평균 (n+1)/2번 비교하고, 탐색이 실패할 경우 n번 비교합니다. 시간복잡도는 O(n)입니다.
개선된 순차 탐색
비교 횟수를 줄이는 방법이 있습니다.
int seq_search2(int key, int low, int high) {
int i;
list[high+1] = key;
for (i=low; list[i]!=key; i++)
;
if (i==(high+1)) return -1; // 탐색 실패시
else return i; // 탐색 성공시
}
리스트의 끝에 찾고자 하는 키 값을 저장하고 반복문의 탈출 조건을 키 값을 찾을 때까지로 설정하도록 수정했습니다. 수정된 프로그램은 매번 key 값과 비교하지 않아도 되므로 비교 연산의 수를 반으로 줄일 수 있습니다.
정렬된 배열에서의 탐색
앞에서 보았던 순차 탐색은 배열의 항목이 얼마 되지 않는 경우에는 충분히 가능한 알고리즘입니다. 그러나 배열이 많은 항목을 가지는 경우에는 순차 탐색은 비효율적인 방법입니다. 따라서 훨씬 빠른 방법을 찾아야 합니다. 우선 정렬된 배열일 때를 가정했을 때 순차 탐색을 개선하고 다른 탐색 방법을 찾아봅시다.
키 값보다 큰 항목을 만나면 배열의 마지막까지 검색하지 않고도 탐색 항목이 없음을 알 수 있습니다.
int sorted_seq_search(int key, int low, int high) {
int i;
for (i=low; i<=high; i++)
if (list[i]>key) return -1;
if (list[i]==key) return i;
}
이 방법도 순차 탐색의 근본적인 비효율성을 해결하지 못합니다. 만약 찾고자 하는 항목이 배열의 뒷부분에 존재한다면 원래의 순차 탐색과 거의 차이가 나지 않기 때문입니다. 비교 횟수는 탐색이 성공할 경우 일반 순차 탐색과 동일하지만, 탐색이 실패할 경우에는 비교 횟수가 반으로 줄어듭니다. 시간 복잡도의 차수는 O(n)입니다.
이진 탐색
정렬된 배열의 탐색에는 이진 탐색(binary search)이 가장 적합합니다. 이진 탐색은 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 리스트에 있는지를 알아내어 탐색의 범위를 반으로 줄입니다. 이 방법으로 매 단계에서 검색해야 할 리스트의 크기를 반으로 줄입니다. 이진 탐색을 적용하려면 탐색하기 전에 배열이 반드시 정렬되어야 하므로 데이터의 삽입과 삭제가 빈번할 경우에는 적합하지 않습니다.
재귀 호출을 이용한 이진 탐색
int search_binary(int key, int low, int high) {
int middle;
if (low<=high) { // 아직 검색할 항목이 남아 있으면
middle = (low+high)/2;
if (key==list[middle])
return middle; // 탐색 성공
else if (key<list[middle])
return search_binary(key, low, middle-1); // 왼쪽 부분 리스트 탐색
else if (key>list[middle])
return search_binary(key, middle+1, high); // 오른쪽 부분 리스트 탐색
}
return -1; // 탐색 실패
}
효율성을 위해서는 아래의 반복 구조를 사용하는 것이 낫습니다.
반복을 이용한 이진 탐색
int search_binary2(int key, int low, int high) {
int middle;
while (low<=high) { // 아직 검색할 항목이 남아 있으면
middle = (low+high)/2;
if (key==list[middle])
return middle; // 탐색 성공
else if (key<list[middle])
high = middle-1; // 왼쪽 부분 리스트 탐색
else if (key>list[middle])
low = middle+1; // 오른쪽 부분 리스트 탐색
}
return -1; // 탐색 실패
}
이진 탐색의 시간 복잡도는 O(log2n)이 됩니다.
색인 순차 탐색
색인 순차 탐색(indexed sequential search) 방법은 인덱스라는 테이블을 사용하여 탐색의 효율을 높이는 방법입니다. 인덱스 테이블은 주 자료 테이블에서 일정한 간격으로 발췌한 자료를 가지고 있습니다. 인덱스 테이블에 m개의 항목이 있고, 주 자료 테이블의 데이터 수가 n이면 각 인덱스 항목은 주 자료 테이블의 n/m번째 데이터를 가지고 있습니다.
인덱스 테이블에서 index[i] <= key < index[i+1]을 만족하는 항목을 찾습니다. 위의 조건을 만족하는 항목으로 주 자료 테이블에서 순차 탐색을 수행합니다. 이 방법은 주 자료 테이블에서의 탐색 시간을 상당히 줄일 수 있으므로 파일 처리, 데이터베이스 등의 응용 분야에서 많이 쓰입니다.
int search_index(int key) {
int i, low, high;
if (key<list[0] || key>list[n-1]) // 키 값이 범위 내의 값이 아니면 탐색 종료
return -1;
for (i=0;i<INDEX_SIZE; i++) // 인덱스 테이블을 조사하여 해당 키의 구간 결정
if (index_list[i].key<=key && index_list[i+1].key>key)
break;
if (i==INDEX_SIZE) { // 인덱스 테이블의 끝이면
low = index_list.key[i-1].index;
high = n-1;
}
else {
low = index_list[i].index;
high = index_list[i+1].index-1;
}
return seq_search(key, low, high);
}
탐색 성능은 인덱스 테이블의 크기에 좌우됩니다. 인덱스 테이블의 크기를 줄이면 주 자료 테이블에서의 탐색 시간을 증가시키고, 인덱스 테입르의 크기를 늘이면 인덱스 테이블의 탐색 시간을 증가시킵니다. 시간 복잡도는 O(m+n/m) 입니다.
보간 탐색
보간 탐색(interpolation search)은 사전이나 전화번호부를 탐색하는 방법과 같이 탐색 키가 존재할 위치를 예측하여 탐색하는 방법입니다. 보간 탐색은 이진 탐색과 유사하나 리스트를 반으로 분할하지 않고 불균등하게 분할하여 탐색합니다. 보간 탐색에서는 다음과 같이 가중치를 주어 탐색 위치를 결정합니다.
탐색 위치 = (k-list[low]) / (list[high]-list[low]) * (high-low) + low
주의해야 할 점은 계산한 값은 일반적으로 실수라는 점입니다. 이 값을 정수로 변환해야 합니다.
int search_interpolation(int key, int n) {
int low, high, j;
while ((list[high]>=key) && (key>list[low])) {
j = ((float)(key-list[low])/(list[high-list[low]])*(high-low))+low;
if (key>list[j]) low=j+1;
else if (key<list[j]) high=j-1;
else low=j;
}
if (list[low]==key) return low; // 탐색 성공
else return -1; // 탐색 실패
}
많은 데이터가 비교적 균등하게 분포되어 있을 경우 보간 탐색은 이진 탐색보다 우수한 방법이 될 수 있으며 시간 복잡도는 O(log2n)이 됩니다.
해싱 탐색
해싱은 키 값에 직접 산술 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산하여 항목에 직접 접근합니다. 이렇게 연산으로 접근하는 구조를 해시 테이블(hash table)이라 부르며, 해시 테이블을 이용한 탐색을 해싱(hashing)이라고 합니다.
해싱은 이론적으로는 O(1)의 시간 안에 탐색을 끝마칠 수 잇습니다. 해싱은 보통 사전(dictionary)와 같은 자료 구조를 구현할 때 좋습니다.
해싱 구조
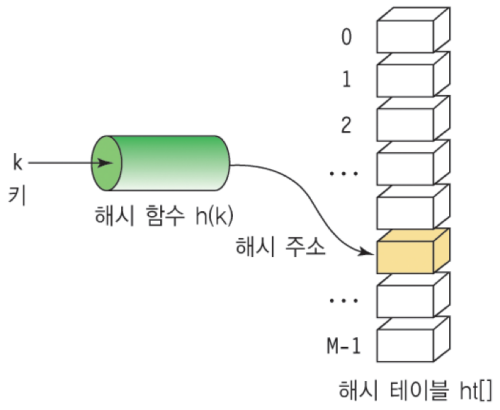
기본적인 아이디어는 간단합니다. 만약 탐색 키들이 0부터 999까지의 정수라고 가정하면 1000개의 요소를 가지고 배열을 만들면 됩니다. 현실적으로 탐색 키들이 문자열이거나 매우 큰 숫자이기 때문에 탐색 키를 직접 배열의 인덱스로 사용하기 힘듭니다. 따라서 각 탐색 키를 작은 정수로 mapping 시켜야 합니다.
해시 함수(hash function)란 탐색 키를 입력으로 받아 해시 주소(hash address)를 생성하고 이 해시 주소가 배열로 구현된 해시 테이블의 인덱스가 됩니다.

해시 테이블 ht는 M개의 버켓(bucket)으로 이루어지는 테이블입니다. 하나의 버켓은 s개의 슬롯(slot)을 가질 수 있으며, 하나의 슬롯에 하나의 항목이 저장됩니다. 하나의 버켓에 여러 개의 슬롯을 두는 이유는 서로 다른 두 개의 키가 해시 함수에 의해 동일한 해시 주소로 변환될 수 있기 때문입니다. 그러나 대부분의 경우 하나의 버켓은 하나의 슬롯을 가집니다.

만약 서로 다른 탐색 키가 같은 해시 주소로 mapping 된다면 문제가 생깁니다. 탐색 키 k1, k2에 대하여 h(k1) = h(k2)인 경우를 충돌(collision)이라고 하며, 이러한 키 k1, k2를 동의어(synonym)이라고 합니다. 충돌이 발생하면 같은 버켓에 있는 다른 슬롯에 저장하며 충돌이 빈번하면 버켓 내부의 순차 탐색 시간이 길어지므로 주의해야 합니다.
버켓에 더 이상 항목을 저장할 수 없을 경우 overflow가 발생합니다. 이 때는 더 이상 항목을 저장할 수 없으므로 반드시 해결해야 합니다. 충돌 해결책을 살펴보기 전에 해시 함수를 살펴보고 갑시다.
해시 함수
해시 함수를 잘 설계해야 탐색의 효율도 증대됩니다. 좋은 해시 함수의 조건은 다음의 3가지입니다.
- 충돌이 적어야 한다.
- 해시 함수 값이 해시 테이블의 주소 영역 내에서 고르게 분포되어야 한다.
- 계산이 빨라야 한다.
제산 함수
나머지 연산자(mod)를 사용하는 방식입니다. 탐색 키 k, 테이블의 크기가 M일 때 해시 함수는 다음과 같이 정의 합니다.
h(k) = k mod M
한쪽으로 편중된 주소를 가지지 않기 위해서 테이블의 크기 M은 주로 소수로 택합니다.
폴딩 함수
탐색 키를 여러 부분으로 나누어 모두 더한 값을 해시 주소로 사용합니다. 탐색 키를 나누고 더하는 방법에는 이동 폴딩(shift folding)과 경계 폴딩(boundary folding)이 대표적입니다. 전자의 방식은 탐색 키를 여러 부분으로 나눈 값들을 더하여 해시 주소로 사용하고, 후자의 방법은 탐색 키의 이웃한 부분을 거꾸로 더하여 해시 주소로 사용합니다.

폴딩 함수는 탐색 키가 해시 테이블의 크기보다 더 큰 정수일 때 사용합니다. 예를 들어 탐색 키는 32비트고 해시 테이블의 인덱스가 16비트일 경우를 생각해봅시다. 탐색 키의 앞 16비트를 무시하고 뒤 16비트를 해시 코드를 사용한다면, 이 반대의 경우와 충돌이 발생할 수 있습니다. 따라서 탐색 키의 일부만 사용하는 것을 지양하고 탐색 키를 몇 개의 부분으로 나누어 더하거나 XOR 연산을 사용하는 방식(이를 folding이라 함)이 바람직합니다.
중간 제곱 함수
탐색 키를 제곱한 다음, 중간의 몇 비트를 취해서 해시 주소를 생성합니다. 제곱한 값들의 중간 비트들은 대개 탐색 키의 모든 문자들과 관련이 있기 때문에 충돌이 발생할 확률이 낮고 비교적 고르게 분산됩니다.
비트 추출 방법
해시 테이블의 크기가 M=2k일 때 탐색 키를 이진수로 간주하여 임의의 위치의 k개의 비트를 해시 주소로 사용하는 방법입니다. 간단하지만 일부 정보만을 사용하므로 해시 주소의 집중 현상이 일어날 수 있습니다.
숫자 분석 방법
숫자로 구성된 키에서 각각의 위치에 있는 수의 특징을 미리 알고 있을 경우 편중되지 않은 수들을 조합하여 해시 주소로 사용하는 방법입니다. 예를 들어 학번이 20201001라면 입학년도를 의미하는 앞의 4자릿수는 제외한 나머지 수를 조합하여 해시 주소로 사용할 수 있습니다.
탐색 키가 문자열일 경우
- 문자열에 정수를 할당하는 방법. ex) ‘a’부터 ‘z’에 1부터 26의 숫자를 부여함.
- 문자의 아스키 코드 값이나 유니 코드 값을 사용하는 방법. » “area”와 “academy”를 구별할 수 없음
- 각 문자의 아스키 코드 값을 모두 더하는 방법. » “are”과 “ear”를 구별할 수 없음. 자릿수가 고정됐을 경우, 해시 주소가 편중됨.
충돌 해결법
충돌을 해결할 수 있는 2가지 방법인 선형 조사법과 체이닝에 대해 살펴봅시다.
선형 조사법
선형 조사법(Linear probing)은 특정 버켓에서 충돌이 발생하면 해시 테이블에서 비어 있는 버켓을 찾는(probing) 방법입니다. 만약 ht[k]에서 충돌이 발생한다면, ht[k+1]부터 차례로 조사하여 ht[k+2], ht[k+3] … 과 같이 선형적으로 조사합니다. 테이블에 끝에 다다랐다면 ht[0]부터 조사합니다.
크기가 7인 해시 테이블에 8, 1, 9, 6, 13 순서대로 탐색 키를 저장하는 예제입니다. 해시 함수는 h(k) = k mod 7입니다.
- 8 저장: h(8) = 8 mod 7 = 1 (저장)
- 1 저장: h(1) = 1 mod 7 = 1 (충돌) » (h(1)+1) mod 7 = 2 (저장)
- 9 저장: h(9) = 9 mod 7 = 2 (충돌) » (h(9)+1) mod 7 = 3 (저장)
- 6 저장: h(6) = 6 mod 7 = 6 (저장)
- 13 저장: h(13) = 13 mod 7 = 6 (충돌) » (h(13)+1) mod 7 = 0 (저장)
선형 조사법 예제
다음 탐색 키들이 삽입 된다고 가정해봅시다.
“do”, “for”, “if”, “case”, “else”, “return”, “function”

“case”, “else”, “return”와 “if”, “function”이 같은 해시 주소를 가짐을 알 수 있습니다.
아래 삽입이 끝난 후 테이블을 봅시다.

한 번 충돌이 시작되면 그 위치에 항목들이 집중되는 군집화(clustering) 현상을 관찰할 수 있습니다.
선형 조사법 구현
#define KEY_SIZE 10 // 탐색 키의 최대 길이
#define TABLE_SIZE 13 // 해시 테이블의 크기
#define empty(e) (strlen(e.key)==0)
#define equal(e1, e2) (!strcmp(e1.key, k2.key))
typedef struct {
char key[KEY_SIZE];
} element;
element hash_table[table]; // 해시 테이블
void init_table(element ht[]) { // 해시 테이블 초기화
int i;
for (i=0; i<TABLE_SIZE; i++) {
ht[i].key[0] = NULL;
}
}
int transform(char *key) { // 탐색 키를 정수로 변환
int number=0;
while(*key)
number += *key++;
return number;
}
int hash_function(char *key) { // 해시 함수
return transform(key) % TABLE_SIZE;
}
void hash_lp_add(element item, element ht[]) { // 삽입
int i, hash_value;
hash_value = i = hash_function(item.key);
while(!empty(ht[i])) { // 버켓이 비어있는지 검사함
if (equal(item, ht[i])) { // 두 항목이 동일한지 검사함
fprintf(stderr, "탐색 키가 중복되었습니다\n");
return;
}
i = (i+1) % TABLE_SIZE;
if (i==hash_value) { // 시작 주소로 되돌아왔을 경우
fprintf(stderr, "테이블이 가득찼습니다\n");
return;
}
}
ht[i]=item;
}
void hash_lp_search(element item, element ht[]) { // 테이블에 저장된 키 탐색
int i, hash_value;
hash_value = i = hash_fuction(item.key);
while (!empty(ht[i])) {
if (equal(item, ht[i])) {
fprintf(stderr, "탐색성공: 위치 = %d\n, "i);
return;
}
i = (i+1) % TABLE_SIZE;
if (i==hash_value) {
fprintf(stderr, "찾는 값이 테이블에 없음\n");
return;
}
}
fprintf(stderr, "찾는 값이 테이블에 없음\n");
}
void hash_lp_print(element ht[]) { // 테이블 출력
int i;
for (i=0; i<TABLLE_SIZE; i++)
printf("[%d] %s\n", i, ht[i].key);
}
void main() {
element tmp;
int op;
while (1) {
printf("원하는 연산을 입력하시오(0: 입력, 1: 탐색, 2: 종료): ");
scanf("%d", &op);
if (op == 2) break;
printf("키를 입력하시오: ");
scanf("%s", tmp.key);
if (op == 0)
hash_lp_add(tmp, hash_table);
else if (op == 1)
hash_lp_search(tmp, hash_table);
hash_lp_print(hash_table);
}
}
이차 조사법
이차 조사법 (quadratic probing)은 선형 조사법과 비슷하지만, 다음 조사할 위치를 아래의 식으로 결정합니다.
(h(k)+inc*inc) mod M for inc=0,1, …, M-1
따라서 조사 위치는 다음과 같습니다.
h(k), h(k)+1, h(k)+4, h(k)+9 …
모든 위치를 조사할 수 있으려면 테이블 크기는 선형 조사법과 동일하게 소수여야 합니다. 하지만 군집화 현상을 완화할 수 있습니다. 동일한 위치로 mapping되는 여러 탐색 키들이 같은 순서로 버켓을 조사하지만 다음에 소개할 이중 해시법으로 해결할 수 있습니다.
이차 조사법 구현
void hash_qp_add(element item, element ht[]) {
int i, hash_value, inc=0;
hash_value = i = hash_function(item.key);
while(!empty(ht[i])) {
if (equal(item, ht[i])) { // 두 항목이 동일한지 검사함
fprintf(stderr, "탐색 키가 중복되었습니다\n");
return;
}
i = (hash_value+inc*inc) % TABLE_SIZE; // i 대신 hash_table 사용, next step
inc = inc + 1;
if (i==hash_value) { // 시작 주소로 되돌아왔을 경우
fprintf(stderr, "테이블이 가득찼습니다\n");
return;
}
}
ht[i]=item;
}
}
이중 해싱법 or 재해싱
이중 해싱법(double hashing) or 재해싱(rehashing)은 오버플로가 발생하면 원래 해시 함수와 별개의 해시 함수를 이용하는 방법입니다. 탐색 키를 참조하여 조사 순서를 결정하므로 함수 값이 같다면 차후 조사값들이 동일하다는 선형 조사법의 문제점을 해결할 수 있습니다.
두 번째 해시 함수는 조사 간격을 결정합니다.
step = C - (k mod C) (C는 테이블의 크기보다 약간 작은 소수)
조사 위치는 다음과 같습니다.
h(k), h(k)+step* 1, h(k)+step* 2, h(k)+step* 3 …
이중 해싱법 구현
void hash_qp_add(element item, element ht[]) {
int i, hash_value, inc=0;
hash_value = i = hash_function(item.key);
inc = hash_function2(item.key); // step 결정
while(!empty(ht[i])) {
if (equal(item, ht[i])) { // 두 항목이 동일한지 검사함
fprintf(stderr, "탐색 키가 중복되었습니다\n");
return;
}
i = (i+inc) % TABLE_SIZE; // next step
inc = inc + 1;
if (i==hash_value) { // 시작 주소로 되돌아왔을 경우
fprintf(stderr, "테이블이 가득찼습니다\n");
return;
}
}
ht[i]=item;
}
}
체이닝
체이닝 (chaining)은 해시 테이블의 구조를 변경하여 각 버켓이 하나 이상의 값을 저장할 수 있도록 연결리스트를 할당하는 방법힙니다.
크기가 7인 해시 테이블에 8, 1, 9, 6, 13 순서대로 탐색 키를 저장하는 예제입니다. 해시 함수는 h(k) = k mod 7입니다.
- 8 저장: h(8) = 8 mod 7 = 1 (저장)
- 1 저장: h(1) = 1 mod 7 = 1 (충돌) » 새로운 노드 생성 및 저장
- 9 저장: h(9) = 9 mod 7 = 2 (저장)
- 6 저장: h(6) = 6 mod 7 = 6 (저장)
- 13 저장: h(13) = 13 mod 7 = 6 (충돌) » 새로운 노드 생성 및 저장
항목의 중복을 허용할 것인지에 따라 연결 방법을 결정할 수 있습니다. 만약 중복을 허용한다면 연결리스트의 처음에다 삽입하는 것이 효율적입니다. 중복이 허용되지 않는다면, 연결리스트를 전부 탐색해야 하므로 연결리스트의 끝에 삽입하는 것이 자연스럽습니다.
체이닝 구현
#define KEY_SIZE 10 // 탐색 키의 최대 길이
#define TABLE_SIZE 13 // 해시 테이블의 크기
#define equal(e1, e2) (!strcmp(e1.key, k2.key))
typedef struct {
char key[KEY_SIZE];
} element;
element hash_table[table]; // 해시 테이블
typedef struct ListNode {
element item;
struct ListNode *link;
} ListNode;
ListNode *hash_table[TABLE_SIZE];
void hash_chain_add(element item, ListNode* ht[]) { // 삽입
int hash_value = hash_function(item.key);
ListNode *ptr; // 새로운 노드
ListNode *node_before = NULL; // 이전 노드
ListNode *node = ht[hash_value]; // 현재 노드
for(; node; node_before=node, node=node->link) {
if (equal(node->item, item)) {
fprintf(stderr, "이미 탐색 키가 저장되어 있음\n");
return;
}
}
ptr = (ListNode*)malloc(sizeof(ListNode));
ptr->item = item;
ptr->link = NULL;
if (node_before) // 기존의 연결 리스트가 있으면
node_before->link = ptr;
else // 기존의 연결 리스트가 없으면
ht[hash_value] = ptr;
}
void hash_chain_find(element item, ListNode *ht[]) { // 탐색
ListNode *node;
int hash_value = hash_function(item.key);
for (node=ht[hash_value]; node; node=node->link) {
if (eqaul(node->item, item)) {
printf("키를 찾았음\n");
return;
}
}
printf("키를 찾지 못했음\n");
}
탐색 성능 비교
| 탐색 방법 | 탐색 | 삽입 | 삭제 |
|---|---|---|---|
| 순차 탐색 | O(n) | O(1) | O(n) |
| 이진 탐색 | O(log 2n) | O(+n) | O(+n) |
| 해싱(최선의 경우) | O(1) | O(1) | O(1) |
| 해싱(최악의 경우) | O(n) | O(n) | O(n) |
| 이진 탐색 트리(균형) | O(log 2n) | O(log 2n) | O(log 2n) |
| 이진 탐색 트리(경사) | O(n) | O(n) | O(n) |
출처
C언어로 쉽게 풀어쓴 자료 구조, 천인국 저