목차
트리
이제까지는 리스트, 스택, 큐 등의 선형 자료 구조(linear data structure)만을 소개했습니다. 이 챕터에서는 hierarchical structure인 자료를 표현하는 트리(tree)를 살펴보겠습니다.
용어 소개
기본적인 용어를 먼저 알아봅시다.
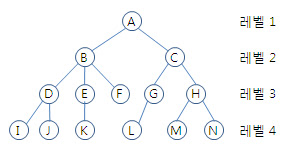
- 노드(node)
트리를 구성하는 기본 원소
예제) A, B, C, D, E, F, G, H, I, J, K, L, M, L - 트리(tree)
한 개 이상의 노드로 이루어진 유한 집합 - 루트 노드(root node)
계층 구조에서 가장 높은 곳에 있는 노드
예제) A - 서브 트리(subtree)
루트 노드를 제외한 노드
예제) {B, D, E, F, I, J, K}, {C, G, H, L, M, N}
서브 트리인 {B, D, E, F, I, J, K}의 루트는 B이고 나머지 노드는 다시금 {D, I, J}, {E, K}, {F}로 나뉩니다. - 간선(edge)
노드와 노드 간의 연결선 - 자식(children), 부모(parent), 형제(brother/sibling) 노드
예제) B의 자식은 D
예제) D의 부모는 B
예제) D의 형제는 E, F - 조상(ancestor)
루트 노드에서 임의의 노드까지의 경로를 이루고 있는 노드
예제) K의 조상은 A, B, E - 자손(descendent) 노드
임의의 노드 하위에 연결된 모든 노드
예제) C의 자손은 G, H, L, M, N - 노드의 차수(degree)
어떤 노드가 가지고 있는 자식 노드의 개수
예제) B의 degree는 3 - 트리의 차수
트리가 가지고 있는 노드의 degree 중 가장 큰 degree 예제) 트리의 degree = 3 - 단말(terminal/leaf) 노드
자식 노드가 없는 노드(degree가 0인 노드)
예제) I, J, K, L, M, N - 비단말(nonterminal) 노드
자식 노드가 있는 노드(degree가 0이 아닌 노드)
예제) A, B, C, D, E, F, G, H - 트리의 레벨(level)
트리의 각 층에 번호를 매겨 루트의 레벨을 1로 두고 한 층씩 내려갈수록 1씩 증가합니다. - 노드의 깊이(depth)
루트에서 어떤 노드까지의 경로 길이
예제) D의 depth = 2 - 트리의 높이(height)
트리가 가지고 있는 최대 레벨
예제) 트리의 height = 4 - 숲(forest)
트리들의 집합
이진 트리
순서 트리, 균형 트리 등 다양한 트리가 있지만 여기서는 이진 트리만 살펴보도록 하겠습니다. 이진 트리(binary tree)란 모든 노드의 degree가 2 이하인 순서 트리(각 자식 노드에 순서가 부여되어 저장 위치가 고정된 트리)를 말합니다. 서브 트리간의 순서가 존재한다는 점, 이진 트리의 서브 트리도 이진 트리의 성질을 만족해야 한다는 점을 잘 생각해봅시다.
이진 트리의 성질
이진 트리의 분류
이진 트리의 표현 방법
이진 트리를 표현하는 두 가지 방법이 있습니다. 하나씩 살펴봅시다.
배열 표현법

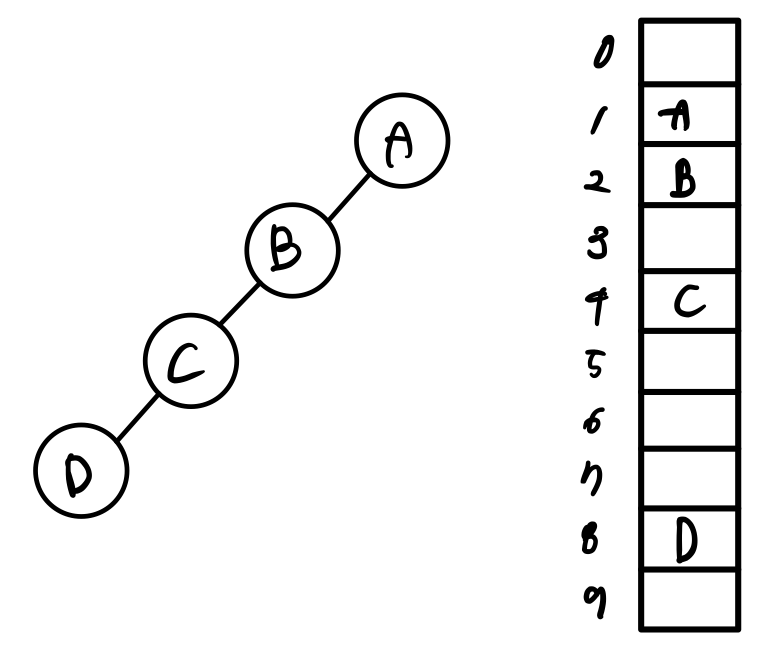
위의 예제는 노드들은 먼저 번호가 매겨진 다음, 번호에 따라서 배열에 저장됩니다. 왼쪽의 완전 이진 트리를 보면 노드 A는 번호가 1이므로 배열의 인덱스 1에 저장합니다. 노드 B는 번호가 2이므로 배열의 인덱스 2에 저장합니다. 인덱스 0은 사용하지 않습니다.
오른쪽의 완전 이진 트리가 아닌 일반 이진 트리에서도 저장은 가능하지만 메모리 공간의 낭비가 큽니다. 따라서 이 방법은 주로 포화 이진 트리나 완전 이진 트리에서 많이 쓰입니다.
배열 표현법에서는 인덱스를 통해 노드의 부모 자식 관계를 알 수 있습니다.
- 노드 i의 부모 노드 인덱스 = i/2
- 노드 i의 왼쪽 자식 노드 인덱스 = 2i
- 노드 i의 오른쪽 자식 노드 인덱스 = 2i+1
링크 표현법
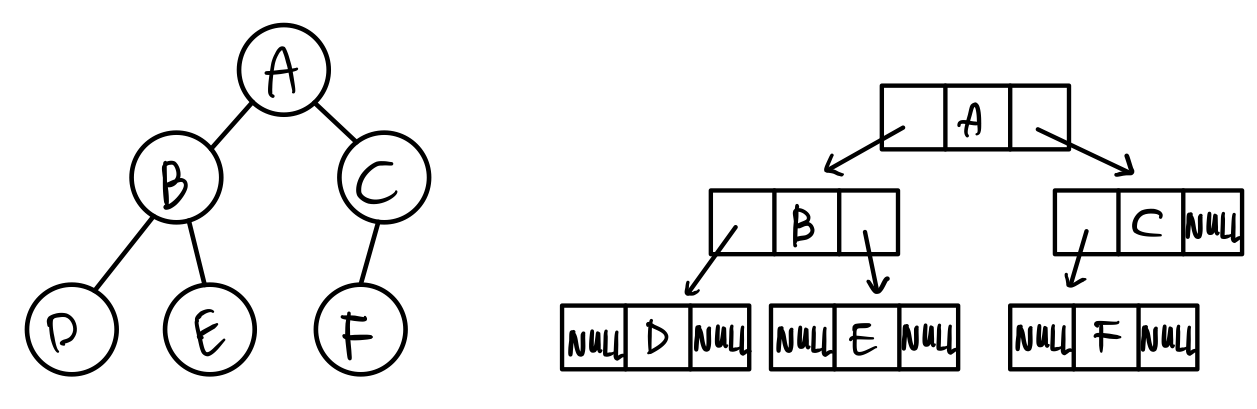

이 방법은 노드가 구조체로 표현되고, 각 노드가 데이터를 저장하는 필드와 자식을 가리키는 2개의 포인터를 가지고 있습니다. 이 구조를 아래처럼 구현할 수 있습니다.
typedef struct TreeNode {
int data;
struct TreeNode *left, *right;
} TreeNode;
int main() {
TreeNode *n1, *n2, n3;
n1 = (TreeNode *) malloc(sizeof(TreeNode));
n2 = (TreeNode *) malloc(sizeof(TreeNode));
n3 = (TreeNode *) malloc(sizeof(TreeNode));
n1 -> data = 10;
n1 -> left = n2;
n1 -> right = n3;
n2 -> data = 20;
n2 -> left = NULL;
n2 -> right = NULL;
n3 -> data = 30;
n3 -> left = NULL;
n3 -> right = NULL;
}
이진 트리의 순회
출처
C언어로 쉽게 풀어쓴 자료 구조, 천인국 저
정보통신기술용어 해설